- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модель <GI₃|GI|1> презентация
Содержание
- 1. Модель <GI₃|GI|1>
- 2. Модель 1 2
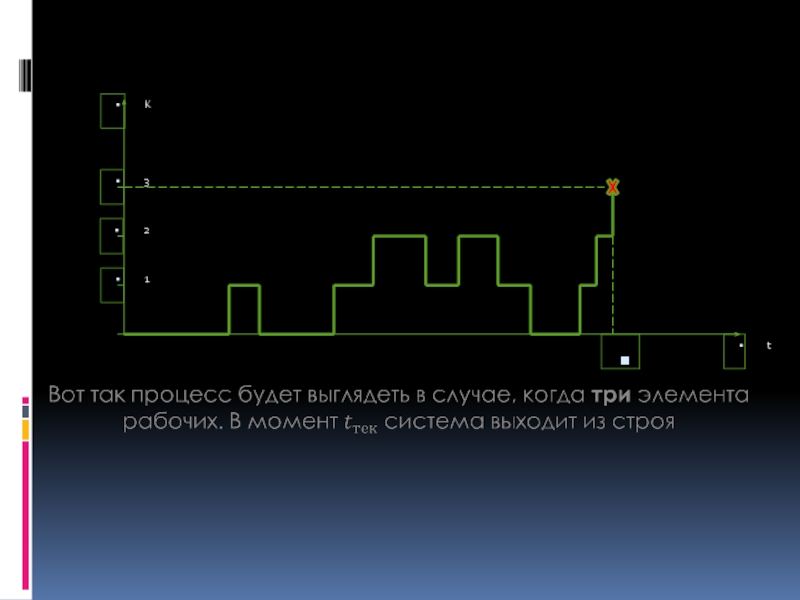
- 3.
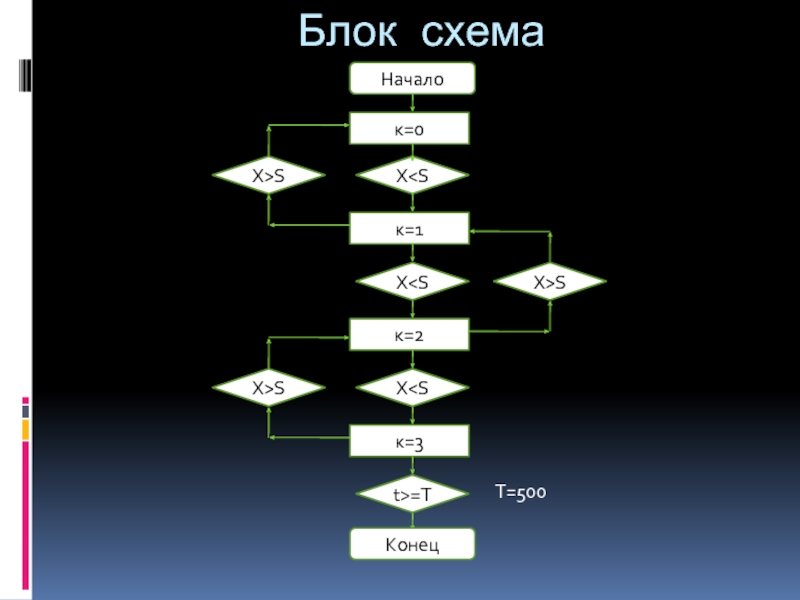
- 4. Блок схема Начало к=0 XS XS XS t>=T T=500
- 5. Стационарные вероятности Если разделить время, которое система
- 6. Стационарные вероятности, вычисленные аналитически Вероятность состояний имеет вид: Тогда
- 7. Сравним стационарные вероятности, рассчитанные аналитически и получившиеся после моделирования
- 8. Модель для 1 рабочего Видим, что за
- 9. Модель для 2 рабочего Видим, что за
- 10. Вывод По моей модели с данными параметрами
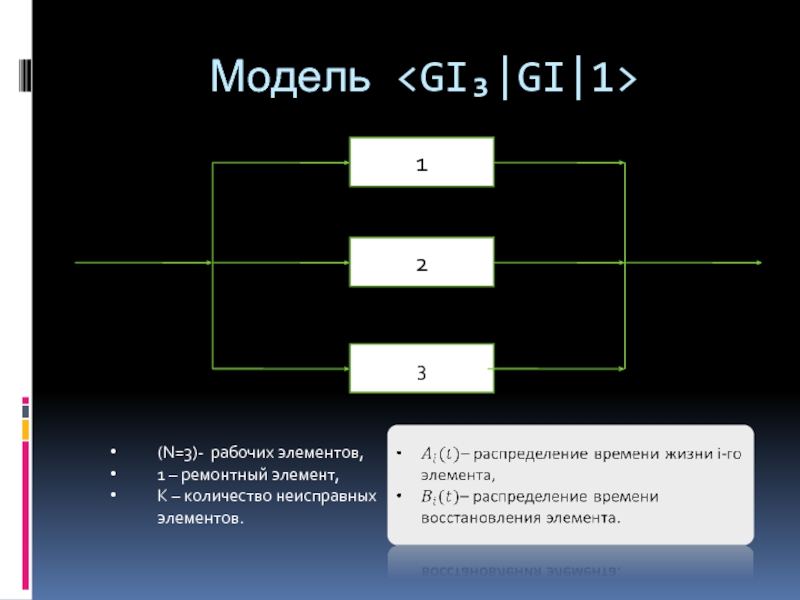
Слайд 2 Модель
1
2
3
(N=3)- рабочих элементов,
1 – ремонтный элемент,
К
– количество неисправных элементов.
Слайд 5Стационарные вероятности
Если разделить время, которое система находится в k-ом состоянии на
все время жизни системы, то мы найдем стационарную вероятность нахождения системы в k-ом состоянии. Тогда получим:
P:=[0.9051, 0.0882, 0.0067, 0.00059]
p₀-вероятность того, что количество элементов вышедших из строя равно нулю
p₁-вероятность того, что количество элементов вышедших из строя равно одному
p₂-вероятность того, что количество элементов вышедших из строя равно двум
p₃-вероятность того, что система вышла из строя
P:=[0.9051, 0.0882, 0.0067, 0.00059]
p₀-вероятность того, что количество элементов вышедших из строя равно нулю
p₁-вероятность того, что количество элементов вышедших из строя равно одному
p₂-вероятность того, что количество элементов вышедших из строя равно двум
p₃-вероятность того, что система вышла из строя
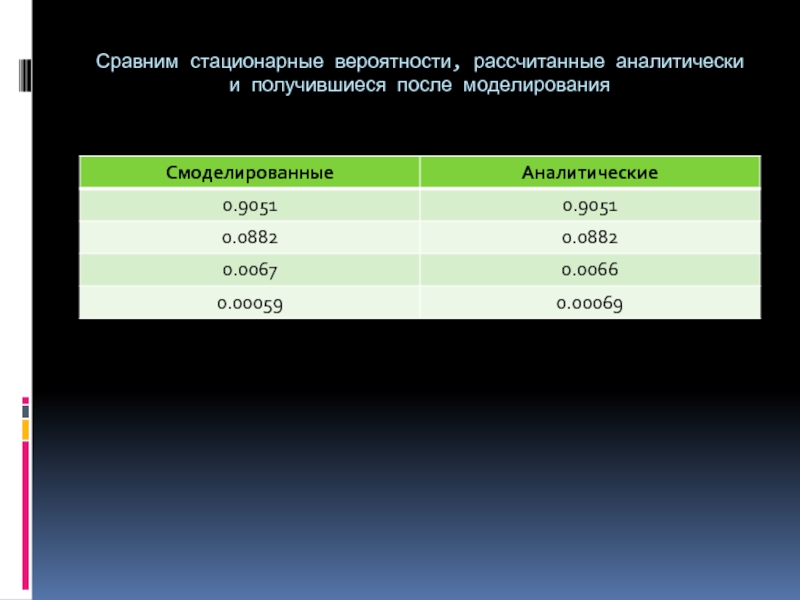
Слайд 7Сравним стационарные вероятности, рассчитанные аналитически и получившиеся после моделирования
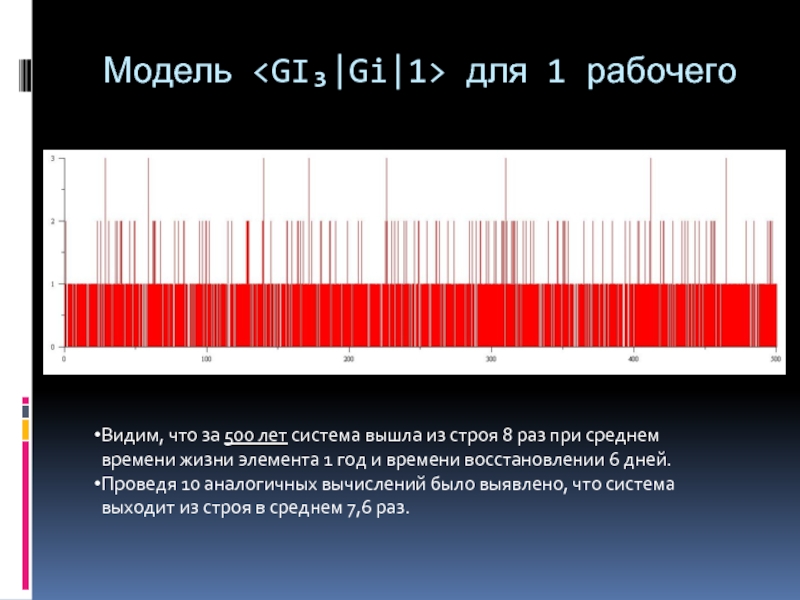
Слайд 8Модель для 1 рабочего
Видим, что за 500 лет система вышла
из строя 8 раз при среднем времени жизни элемента 1 год и времени восстановлении 6 дней.
Проведя 10 аналогичных вычислений было выявлено, что система выходит из строя в среднем 7,6 раз.
Проведя 10 аналогичных вычислений было выявлено, что система выходит из строя в среднем 7,6 раз.
Слайд 9Модель для 2 рабочего
Видим, что за 5000 лет система не
вышла из строя ни разу при среднем времени жизни элемента 1 год и времени восстановлении 6 дней.
Слайд 10Вывод
По моей модели с данными параметрами (3 рабочих элементов с средним
временем жизни 1 год и одним ремонтным элементом с средним временем восстановления 6 дней) можно понять, что данная система будет выходить из строя со средней частотой 7,6 за 500 лет. Чтобы система не выходила из строя ни разу на более продолжительном сроке, нужно ввести еще одного рабочего.